畅通工程
Time Limit: 4000/2000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others) Total Submission(s): 22846 Accepted Submission(s): 11908
Problem Description
某省调查城镇交通状况，得到现有城镇道路统计表，表中列出了每条道路直接连通的城镇。省政府“畅通工程”的目标是使全省任何两个城镇间都可以实现交通（但不一定有直接的道路相连，只要互相间接通过道路可达即可）。问最少还需要建设多少条道路？
Input
测试输入包含若干测试用例。每个测试用例的第1行给出两个正整数，分别是城镇数目N ( < 1000 )和道路数目M；随后的M行对应M条道路，每行给出一对正整数，分别是该条道路直接连通的两个城镇的编号。为简单起见，城镇从1到N编号。 注意:两个城市之间可以有多条道路相通,也就是说 3 3 1 2 1 2 2 1 这种输入也是合法的 当N为0时，输入结束，该用例不被处理。
Output
对每个测试用例，在1行里输出最少还需要建设的道路数目。
Sample Input
4 2 1 3 4 3 3 3 1 2 1 3 2 3 5 2 1 2 3 5 999 0 0
方法一：并查集算法
并查集是一种树型的数据结构。用于处理一些不相交集合（Disjoint Sets）的合并及查询问题。
并查集一般就三个操作：初始化，查找，合并。 一般都是用一个一维数组来组织，数组所存内容为该下标表示点的父节点(实际是一棵树，每个结点都指向父节点，用根节点来标志集合)。
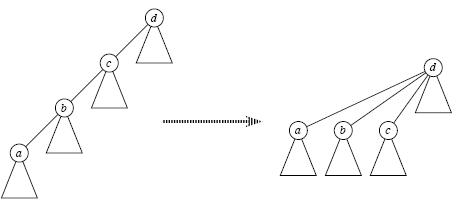
1,初始化函数一般没有什么变化，都是将每个结点的父节点初始化为本身； 2,查找函数一般都是递归的寻找父节点直至根结点，返回根结点的值来标识集合；并查集的优化，路径压缩 寻找祖先时我们一般采用递归查找，但是当元素很多亦或是整棵树变为一条链时，每次find(x)都是O(n)的复杂度，有没有办法减小这个复杂度呢？ 答案是肯定的，这就是路径压缩，即当我们经过"递推"找到祖先节点后，"回溯"的时候顺便将它的子孙节点都直接指向祖先，这样以后再次find(x)时复杂度就变成O(1)了，如下图所示；可见，路径压缩方便了以后的查找。
3,合并函数一般就将两个集合中一个根结点的父节点设为另一个根结点(由这一步使得各个元素合并为一棵树，一开始只是自己指向自己)。
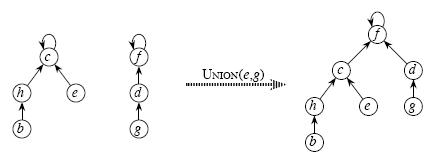优化：按秩合并，秩，即树的高度。 即合并的时候将元素少的集合合并到元素多的集合中，这样合并之后树的高度会相对较小。
import java.util.*;import java.io.*;public class Main { public static ArrayList ay; public static int patten[]; public static int n,m; public static void main(String[] args) { Scanner sc=new Scanner(new BufferedInputStream(System.in)); while(sc.hasNextInt()){ n=sc.nextInt(); if(n==0) break; ay=new ArrayList (); m=sc.nextInt(); for(int i=0;i 0) System.out.println(number); else System.out.println(0); } //并查集合并 public static void union(int aa,int bb){ for(int i=1;i<=n;i++){ if(patten[i]==aa) patten[i]=bb; } }}class Count1{ int a; int b; Count1(int a,int b){ this.a=a; this.b=b; }} 方法二：Kruskal（克鲁斯卡尔算法）
思路： 第一步 排序
第二步 并查集算法
import java.io.*;import java.util.*;public class Main { public static int n,m; public static ArrayList ay; public static int patten[]; public static void main(String[] args) { Scanner sc = new Scanner(new BufferedInputStream(System.in)); while (sc.hasNextInt()) { n = sc.nextInt(); if(n==0) break; m = sc.nextInt(); ay=new ArrayList (); for (int i = 1; i <= m; i++) { int a=sc.nextInt(); int b=sc.nextInt(); int d=i; Count c=new Count(a,b,d); ay.add(c); } Kruskal(); Collections.sort(ay); patten=new int[n+1]; for(int i=1;i<=n;i++){ patten[i]=i; } } } //Kruskal（克鲁斯卡尔算法） public static void Kruskal(){ Collections.sort(ay); patten=new int[n+1]; //并查集初始化 for(int i=1;i<=n;i++){ patten[i]=i; } int count=0; //并查集 查找 for(int i=0;i 0) System.out.println(number); else System.out.println(0); } //并查集合并 public static void union(int j,int k){ for(int i=1;i<=n;i++){ if(patten[i]==j) patten[i]=k; } }}class Count implements Comparable { int a; int b; int d; Count(int a,int b,int d){ this.a=a; this.b=b; this.d=d; } public int compareTo(Count o) { return this.d>o.d?1:-1; }}